신호 탐지 이론
인지심리학에서 매우 중요한 주제 중 하나인 신호탐지이론에 대해서 간단하게 알아보자!
신호탐지이론은 2차 세계대전을 전후해서 레이더 관측병들의 행동을 관찰하면서 발전했다. 당시 레이더가 질이 그리 좋지 않은 것도 있고 해서 지금 화면에 찍힌 게 적인지 노이즈가 지직거리는 건지 알기가 힘들었고, 당연히 관측병이 적이 아닌데도 적이 나타났다고 보고하거나 혹은 적인데도 노이즈라고 생각하고 보고를 안 했다가 폭탄이 떨어졌다거나 하는 일들이 발생했을 것이다. 문제는 이게 관측병을 갈군다고 해결되는 문제가 아니었다는 것이다. 그래도 (모 황군과는 다르게)합리적이었던 미군은 이 문제에 대해서 과학적으로 분석하게 되었고 그렇게 해서 정립된 것이 신호탐지이론이다. 여기서 알 수 있지만 심리학은 상당부분 군대 덕에 발전했다.
그러면 우리 불쌍한 레이더 관측병이 보고 있는 레이더 화면에 점이 하나 찍혔을 때 가능한 경우의 수를 따져보자.
| 적기가 나타났다고 보고 | 보고하지 않음 | |
|---|---|---|
| 적기 맞음 | Hit 적중 | Miss 탈루 |
| 적기 아님 | False Alarm 오경보 | Correct Rejection 정기각 |
용어가 묘하게 군대스러운데 다 군대에서 발전한 이론이라고 그렇다고 한다.
점이 찍힌 걸 보고 적기가 나타났다고 보고했는데 실제로 적기였으면 Hit이고, 실제로는 적기가 아니었다면 False Alarm이다. 점을 보고 적기가 아니고 어디 새라도 날아다닌다고 생각해서 보고를 안 했는데 실제로 새가 레이더 근처에서 날아다니고 있었다고 하면 그건 Correct Rejection이다. 그런데 새가 아니라 실제로 적 폭격기가 폭탄 달고 오고 있었으면 그건 Miss다.
상관 입장에선 당연히 Hit과 Correct Rejection을 늘리고 Miss와 False Alarm을 줄이고 싶을 것이다. Miss가 줄어들어야 자다가 폭탄 맞는 일을 피할 수 있을 것이고 False Alarm이 줄어야 잘 자다가 공습이라고 난리쳐야 하는 상황이 줄어들테니까. 그러면 어떻게 하면 될까? 관측병을 갈구면 될까? 신호탐지이론은 이게 갈군다고 되는 문제가 아니라는 걸 알려준다.
왜 그런지 궁금하니 우리 불쌍한 레이더 관측명의 머리 속을 들여다보자.
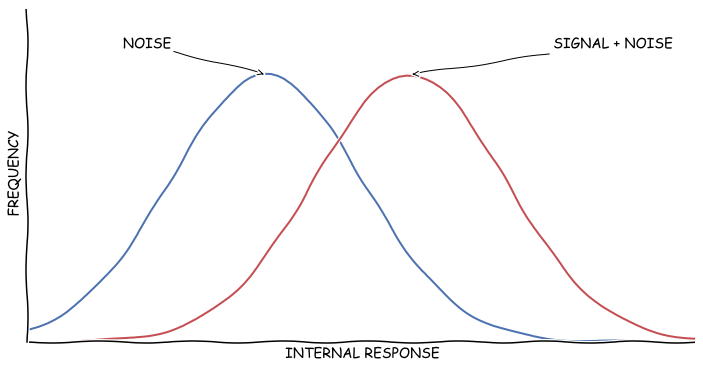
뭔가 재수없는 정규분포가 두 개 튀어나왔다. X축은 레이더 관측병이 느끼는 감각의 강도라고 보면 된다. 그래프를 아주 쉽게 설명하자면, 노이즈만 있을 때는 관측병이 느끼는 감각의 강도가 대충 파란 그래프의 봉우리 근처에서 왔다갔다 한다고 보면 되고, 신호와 노이즈가 섞여 있을 때는 감각의 강도가 빨간 그래프의 봉우리 근처에서 왔다갔다 한다고 보면 된다. 여기서부터 벌써 몇 가지 중요한 사실을 알 수 있다. 노이즈 없이 신호만 있는 경우는 세상에 없고 또 노이즈(어떤 경우에는 자극이 없는 경우에도) 사람은 뭔가 있다고 느낀다는 것이다. 왜 그런지 궁금하면 눈을 한 번 감아보라. 눈 앞에 뭔가 어른거리지 않는가?
자, 레이더 관측병의 감각 구조가 대충 이렇다고 하면, 레이더 관측병은 이런 감각을 느꼈을 때 보고를 할 지 하지 않을지 어떻게 결정할까? 아주 간단하게 표현하면 다음과 같을 것이다:
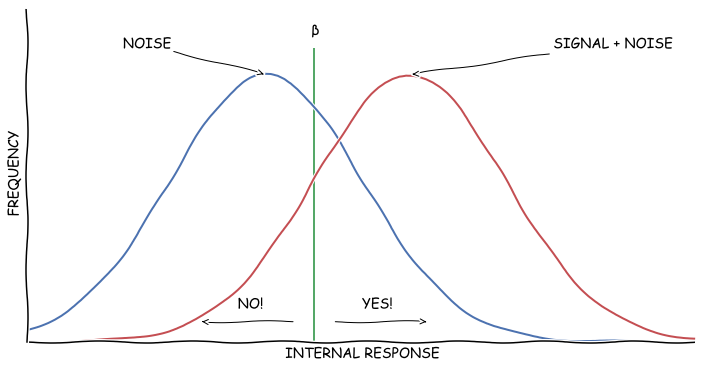
녹색 선이 추가됐다. 녹색 선을 기준으로 해서 녹색 선보다 감각의 강도가 세면 적기다!라고 소리치고, 약하면 새가 날아다니는가보다 뭐 그렇게 생각하고 말자, 이렇게 결정할 수 있다. 이 녹색 선의 위치를 베타$\beta$라고 한다.
자, 이 그래프를 통해서 Miss와 False Alarm이 어떻게 발생하는지 알아보자.
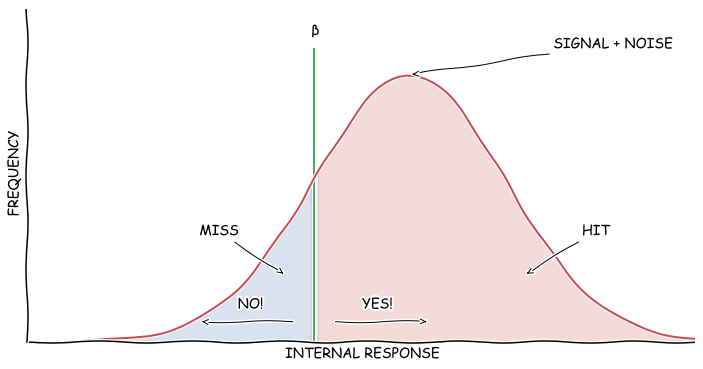
이 그래프도 특별히 어려운 내용은 아니다. 신호가 있을 때(즉 적기가 나타났을 때) 적기가 나타났다고 하면 Hit이고 별 것 아니라고 레이더 화면을 보면서 다시 졸기 시작하면 그건 Miss다.
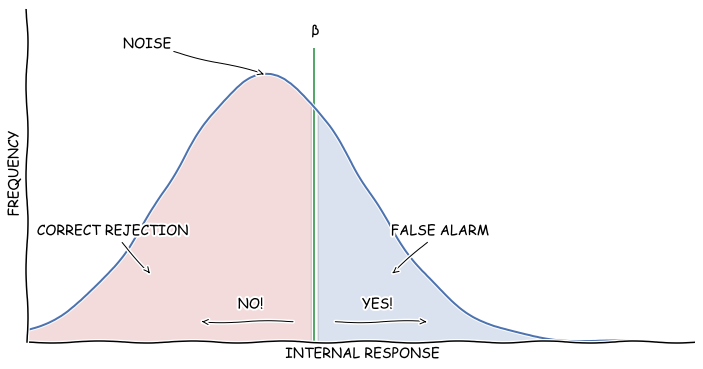
이 그래프도 마찬가지다. 노이즈일 때(그러니까 실제로는 적기가 아닐 때) 적기가 나타났다고 하면 False Alarm이고 그냥 화면이 지직거리는 거라는 옳은 판단을 하면 그건 Correct Rejection이다.
여기서 문제가 보이는가? 앞서 봤던 그래프에서 이 두 개의 정규분포는 겹쳐있었다. 즉 Hit과 Miss와 False Alarm과 Correct Rejection이 막 겹쳐있다는 의미다! 그게 무슨 문제를 야기하는지 구체적으로 살펴보자.
시도때도 없이 난리치지 말라거나, 혹은 정신 똑바로 차리고 화면을 보라거나 하는 식으로 갈구면 베타가 이동한다는 것이 연구를 통해 알려져 있다. 이렇게 겹쳐있는 분포에서 베타가 움직인다는 것은 무슨 의미일까?
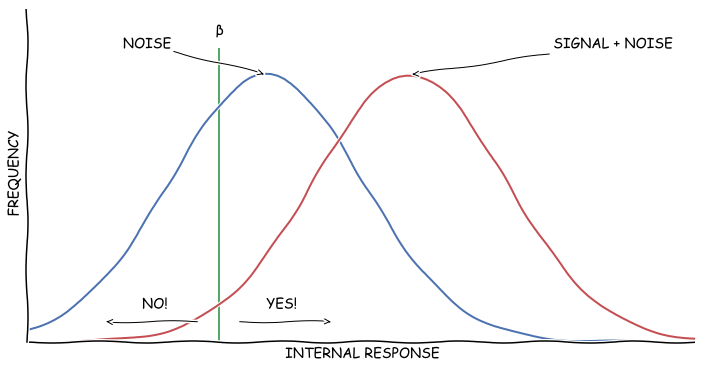
적기를 놓치면 죽는다고 좀 갈궈줬다. 그래서 레이더 관측병의 베타는 왼쪽으로 이동했다. 베타가 왼쪽으로 이동한다는 건 감각의 강도가 약해도 적기가 나타났다고 보고한다는 것이다. 따라서 Hit이 높아지고 Miss는 낮아진다. 그런데 그러면 동시에 False Alarm이 높아지고 Correct Rejection이 낮아진다.
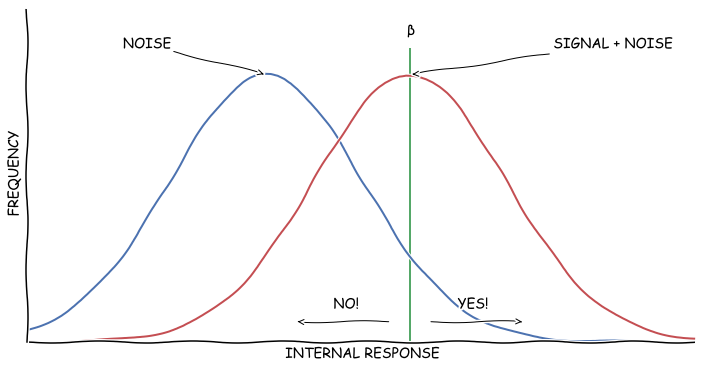
귀찮으니까 시도때도 없이 보고하지 말라고 좀 갈궈줬다. 그러면 레이더 관측병의 베타는 오른쪽으로 이동한다. 베타가 오른쪽으로 이동한다는 건 감각의 강도가 웬만큼 강하지 않은 이상 보고하지 않는다는 의미다. 지휘관이 원했던 것처럼 False Alarm이 줄어들고 Correct Rejection이 높아졌다. 이제 지휘관의 숙면이 방해받지 않을 가능성이 높아졌다! 그렇지만 Miss가 높아지고 Hit이 낮아져 난데없는 폭탄에 비명횡사할 가능성은 높아졌다.
이제 분포가 겹쳐져 있기에 베타를 움직이는 것 가지고는 Miss와 False Alarm을 동시에 줄일 수 없다는 것을 알 수 있다. 그러면 어떻게 해야 할까? 분포가 덜 겹쳐지도록 만들면 된다!
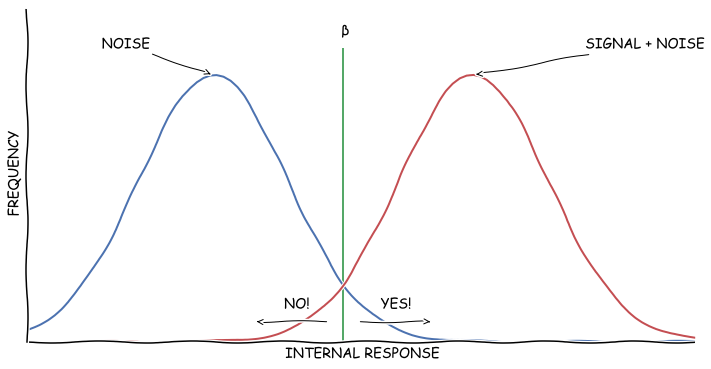
두 분포가 멀리 떨어지니 Miss와 False Alarm의 비율이 낮아졌다! 이게 바로 원하는 결과다. 그래서 두 분포 사이의 거리를 측정하는 기준을 만들었다. 그것이 민감도sensitivity $d'$다.
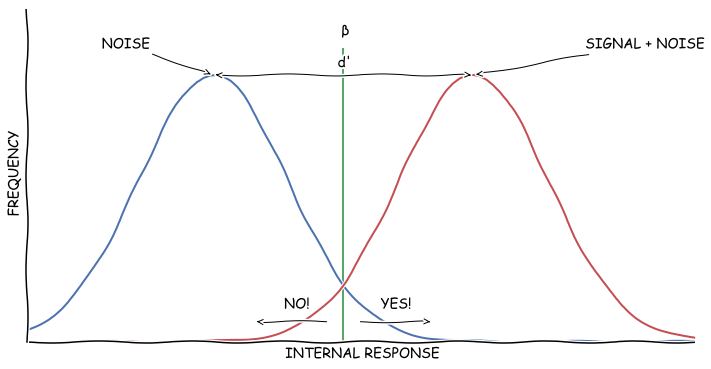
좀 수학적으로 표현하면 $$d'=\frac{\mu_S-\mu_N}{\sqrt{\frac{1}{2}(\sigma_S^2+\sigma_N^2)}}$$ 다. 어떤 사람들은 효과크기를 측정하는 척도인 Cohen’s d $$ d=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{\frac{(n_1-1)s^2+(n_2-1)s_2^2}{n_1+n_2-2}}} $$ 와 닮았다는 것을 느낄지도 모르겠다.
그러면 이 민감도를 높이려면 어떻게 해야할까? 레이더 탐지를 위한 전문 트레이닝을 시킨다던가, 아니면 레이더 장비를 개선한다던가 하는 방법이 있겠다. 휴식을 취하게 해주는 것도 큰 도움이 된다. 여기서도 세상에 공짜란 없다는 것을 새삼 재확인할 수 있다.
