클러스터링과 매니폴드

클러스터링 알고리즘으로 가장 유명한 것은 K-Means일 것이다. K-Means의 문제점은 1. 클러스터의 숫자를 미리 알아야 한다는 것과 2. 클러스터가 구형이라고 가정한다는 것이다. 클러스터가 구형이라는 것은 클러스터를 직관적으로 해석하는데 도움이 된다. Mixture 모형의 구조를 약간 빌려 표현하면, 각 클러스터를 대표하는 가상의 ‘평균’ 혹은 ‘대표’ 포인트가 클러스터의 중심에 존재하고, 그 대표 포인트에서 가장 가까운 데이터 포인트들이 하나의 클러스터로 묶인다고 생각할 수 있다. 그러나 클러스터가 구형이 아닌 경우에는 K-Means로는 클러스터를 제대로 잡아낼 수 없다.

예를 들어 다음과 같은 데이터가 있다고 하자. (HDBSCAN의 예제에서 빌려온 데이터이다. http://nbviewer.jupyter.org/github/scikit-learn-contrib/hdbscan/blob/master/notebooks/Comparing%20Clustering%20Algorithms.ipynb)

위의 데이터에서 클러스터를 6개로 설정하고(6개 정도 있는 것으로 보이지 않는가?) K-Means를 돌려보면 다음과 같은 클러스터가 생성된다.

아마도 기대했던 클러스터와는 클러스터의 형태가 조금 많이 다를 것이다. 이러한 구형이 아닌 클러스터를 포착하기 위해서는 클러스터의 구형성을 가정하지 않는 알고리즘이 필요하다. 그러한 알고리즘인 HDBSCAN을 사용한 결과는 다음과 같다.

직관적으로 기대했던 클러스터와 유사한 결과가 나오지 않는가? (HDBSCAN 짱짱!)

그런데 위와 같이 나타난 클러스터를 어떻게 해석해야 할까? 인간의 시각 기능은 데이터 포인트의 구름에서 쉽게 모양들을 발견해내고 그걸 하나로 묶을 수 있다. 그런데 데이터 포인트가 공간 속에서 어떠한 모양을 가지고 있다고 해서 그 모양을 이루는 데이터 포인트들이 하나의 그룹으로 묶일 수 있다는 보장이 어디 있을까? 다르게 말해서, 데이터 포인트의 모양에 대체 무슨 의미가 있는가?

위의 그림에서 A와 B는 같은 클러스터로 묶이지만 A와 B보다는 B와 D의 거리가 더 가깝다. 그러니까 A와 B는 같은 클러스터지만 다른 점들에 비해서 그 값이 딱히 유사하지 않다. 오히려 많이 다르다고도 할 수 있다. A와 B가 같은 클러스터로 묶이는 근거는 A와 B 사이에 C와 같은 점들이 많이 있다는 것 뿐이다. A와 B의 유사함은 일종의 가족유사성이다. A는 C1과 비슷하고, C1은 C2와 비슷하고, C2는 C3와 비슷하고, C3, … Cn-1은 Cn과 비슷하고, Cn은 B와 유사하다. 따라서 A와 B는 같은 클러스터가 된다. 정작 A와 B는 그렇게 유사하지 않은데도 말이다. 그런데 이런 ‘가족유사성’으로 클러스터를 구성하는 것이 과연 현실적으로 어떤 의미가 있을까?

그런데 사실 이런 식으로 구성한 클러스터가 특별한 의미를 가지는 사례는 아주 흔하다.

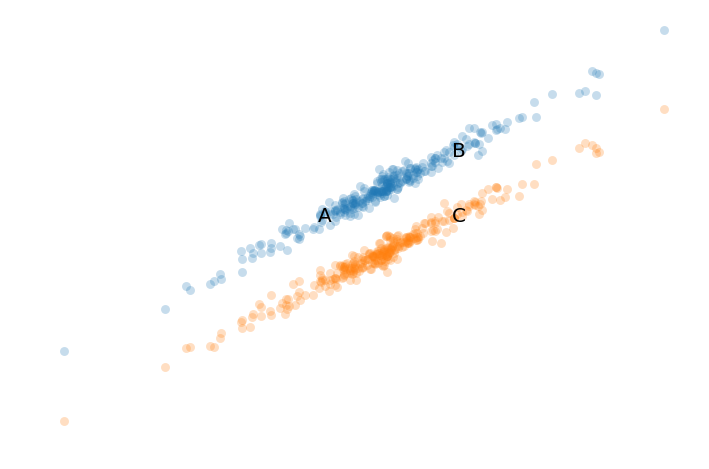
집단을 구분하는 더미 변수를 포함시켜 회귀 분석을 했을 때 흔히 볼 수 있는 그래프다. 여기서 A와 B는 같은 집단에 속하지만 A와 B보다는 B와 C의 거리가 더 가깝다. 그러니까 이런 사례는 아주 흔하게 발생하는 것인 것이다. 흔하게 발생하는 것 이상으로 아주 중요한 현상이라고 할 수 있다. 이와 같이 서로 유사한 점들이 이루는 클러스터 혹은 그룹을 흔히 매니폴드라고 부르고, 현실의 많은 데이터가 실은 이러한 매니폴드 위에 있다는 가정을 매니폴드 가정이라고 부른다.

Noise Rose

Real Rose

256 X 256 컬러 이미지를 256 X 256 X 3 차원의 이미지 공간에 있는 벡터라고 생각하면, 그러한 이미지 공간에 있는 대부분의 이미지 벡터들은 왼쪽과 같은 노이즈 이미지이다. 오른쪽과 같은 ‘유의미한’ 이미지는 사실상 이미지 공간에서 아주 작은 영역에, 혹은 선과 같은 아주 낮은 차원에 밀집되어 있을 것이다.

또한 위와 같은 장미 이미지의 색을 바꾸거나 형태를 조금 바꾸거나 배경을 바꾼다거나 해도 같은 장미 이미지라면, 즉 약간의 변화가 가해져도 여전히 동일한 장미 이미지라면 장미 이미지는 가족유사한, 서로 유사하고 근접해 있음으로 인해 형성된 매니폴드 위에 존재하고 있을 것이다. 장미 이미지라는 특성을 변화시키지 않는 어떤 작은 변화가 이미지 벡터를 이미지 공간에서 약간 움직이는 것이라고 하면 그러한 약간의 변화에도 여전히 장미 이미지인 벡터들이 장미 이미지의 클러스터를 이루고 있을 것이고, 이는 위에서 주위 점들과의 인접성으로 정의된 클러스터 혹은 매니폴드의 정의와 일치한다.

따라서 인간은 상상할 수 없는 높은 차원에 존재하는 데이터 포인트들이 이루는 형태에도 어떤 의미가 있다. 비구형의 클러스터를 발견하는 알고리즘은 그래서 어떤 의미를 가진 클러스터를 발견할 수 있는 것이다.