인과관계를 어떻게 밝힐 수 있는가
우선 인과관계라는 것이 대체 무엇인가? 인과관계라는 것을 명확하게 정의하는 것은 복잡한 철학적 문제다. 그러나 실용적인 목적으로는 단순한 정의를 사용할 수 있다. A를 조작하여 변화시켰을 때 B가 변화한다면 A와 B 사이에는 인과관계가 존재하는 것이다. 즉, A가 B에 (인과적으로) 영향을 미친다고 할 수 있다.
인과관계가 중요한 문제인가? 인과관계 없이도 잘 살 수 있지 않을까? 그러나 우리의 일상적 언어 생활에서, 그리고 각종 의사결정에서 ‘무엇이 무엇 때문에 일어난다’라는 개념이 없어진다고 생각해보자. 우리가 세상에 대해 할 수 있는 말이 얼마나 남게 될까? 그리고 우리가 도대체 어떤 의사결정을 할 수 있게 될까? 인과관계를 배제한다면 남는 것은 A와 B가 상관관계가 있다 정도 밖에 없기 때문이다. (A와 B가 관계가 있다고 말하는 것조차 어렵다. A와 B가 관계가 있다고 하면 흔히 A가 B에 영향을 미치거나 그 반대의 경우에 해당한다고 연상할 수 있기 때문이다.)
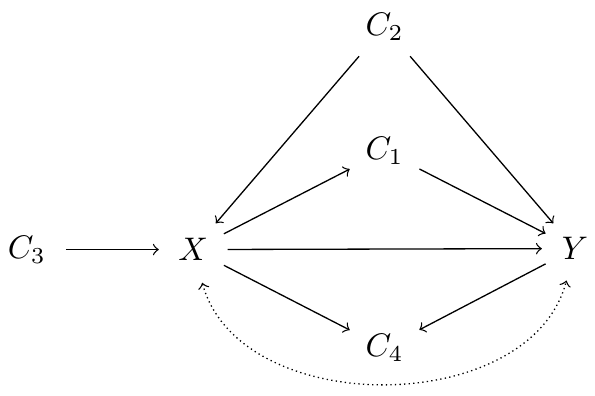
변수들 사이의 인과관계는 도표로 쉽게 나타낼 수 있다. A가 B에 영향을 미친다면 A -> B라고 표기하는 식으로. (점선은 관측되지 않은 변수가 영향을 미치고 있다는 것을 의미한다.) 그리고 이러한 인과관계에 대한 도표(그래프)가 주어진다면 어떤 변수를 관측해야 우리가 원하는 인과관계를 측정하거나 검토할 수 있는지를 알아낼 수 있다. 예를 들어 위의 그래프가 X와 Y 사이의 인과관계를 나타낸다고 하면, X와 Y 사이의 인과관계를 검증하기 위해서는 C1 또는 C3를 관측할 수 있다. (관측되지 않은 변수가 X와 Y에 영향을 미치고 있기 때문에 C2를 관측하는 것은 충분하지 않고, C4는 X -> C <- Y 형태의 구조를 갖고 있기 때문에 C4 를 관측하면 X와 Y 사이에 추가적인 관계가 발생한다.) 다만 X와 Y 사이의 인과적인 관계의 크기를 밝히는 것은 또 다른 문제다.
여하튼 인과관계에 대한 그래프가 주어지면 인과관계를 밝히기 위해 필요한 변수들을 기계적인 절차를 활용하여 알아낼 수 있고, 적절한 데이터가 있다면 인과관계를 밝히는 것이 가능하다. 즉 가정(그래프)이 맞으면 결과도 맞다는 것이다. 가정이 틀렸다면? 결과는 엉망진창이 된다.
그렇다면 이런 인과관계에 대한 그래프를 어떻게 그릴 수 있는가? 이건 데이터만으로 풀 수 있는 종류의 문제가 아니다. 이 그래프를 그리기 위해서는 우리의 추가적인 지식이 필요하다. 우선 고려해야할 변수들을 선정하고, 그 변수들 사이에 우리의 지식을 통해서 인과관계를 설정한다. 그런 구조를 통해 그래프를 그리면 그래프에서 어떤 변수들이 조건부 독립인지를 알아낼 수 있다. (두 변수가 독립Independent이라는 것은 한 변수에 대한 정보가 다른 변수에 대한 정보를 제공하지 않는다는 것을 의미한다. 조건부 독립Conditionally Independent이라는 것은 어떤 변수에 대한 정보가 주어지면, 조건부 독립인 두 변수 중 한 변수에 대한 정보가 다른 변수에 대한 정보를 제공하지 않는다는 것을 의미한다.) 따라서 데이터를 통해 실제로 그 변수들이 조건부 독립인지를 검토할 수 있다. 조건부 독립이 아니라면 우리가 설정한 그래프가 적절하지 않다는 것이다.
그러나 조건부 독립만으로는 그래프를 특정할 수 없다. 특정한 조건부 독립 조건들을 만족하는 그래프는 일반적으로 한 가지가 아니기 때문이다. 즉 같은 조건부 독립 조건을 만족하는 대안 모형이 존재한다. 따라서 대안 모형이 아니라 우리가 채택한 모형이 옳다는 것을 증명해야 한다. 대안 모형들에 포함된 인과관계들이 적절하지 않을 수도 있다. 예를 들어 이후에 일어난 사건에 대한 변수가 이전에 일어난 사건에 영향을 미친다는 식의 인과관계가 포함되어 있을 수 있다. 혹은 여타 다른 방식으로 그 관계들이 말이 되지 않을 수도 있다. 대안적 모형들은 실제 현실을 반영하는 모형에 비해 추가적인 화살표(인과관계)들을 포함하는 경향이 있기 때문에 이러한 기준으로 여러 대안들을 걸러낼 수 있다. 혹은 추가적인 다른 변수들을 도입해서 적절한 모형과 적절하지 않은 모형들을 비교할 수도 있다. 이러한 과정들을 통해 대안적 모형이 아닌 현실을 반영한다고 생각되는 모형을 작성하고 선택할 수 있는 것이다. Pearl은 기존 학계에서 바로 이러한 과정들, 즉 대안 모형들을 고려하는 과정들을 빠뜨리고 있다고 지적한다.
이러한 절차를 따라 그래프를 작성하고 인과관계에 대한 추론을 할 수 있다. 그러나 이론적으로 가능하다는 것이고 수많은 난점들이 존재한다. 어떤 변수를 포함시켜야 하는지는 어떻게 알 수 있을 것이며 그 변수들 사이에 화살표를 어떻게 부여해야 적절한 것인가? 그것은 그 문제에 대한 지식을 통해 해야 하는 것이지만, 그 지식을 활용한다는 것은 수많은 문제를 발생시킬 수 있다. (이러한 문제들 중 일부는 Watts의 상식과 사회학적 설명에 제시되어 있다.) 일단 그래프가 주어진다고 해도, 그 그래프를 검증하기 위해 수많은 변수들 사이의 관계들에 대해 검토해야 하고, 대안 모형들에 대해서도 고찰해야 한다. 즉 한 방에 X와 Y 사이의 관계를 밝힌다는 것은 사실상 불가능하고, 점진적으로 각 변수들 사이의 관계에 대해서 정립해나가고, 그것들을 쌓아나가는 지난한 과정이 필요하다는 것을 의미한다. (물론 분석사회학과 같이 이러한 절차를 적극적으로 지지하는 입장 또한 존재한다.)
거기에 인과관계가 존재한다는 것을 검증하는 것이 아니라 인과관계의 크기, 즉 X가 Y에 얼마나 영향을 미치는가를 밝히기 위해서는 일반적으로 더 많은 변수를 고려해야 한다. 또한 더 나은 의사결정을 위해서는 그렇게 얻어낸 인과관계의 크기에 대한 불확실성에 대한 추정치가 필요하고, 이제 더 복잡한 방법적 도구가 필요해진다. Watts의 주장을 받아들인다면, 이런 절차를 도입한다는 것 자체가 근본적으로 불가능한 문제들도 많이 존재한다.
이런 온갖 문제들 때문에 인과관계를 밝힌다는 것은, 꼭 필요하지만, 정말 지난하고 어려운 과정이다. 그냥 (내 생각에, 혹은 상식적으로) 이게 이렇게 해서 이렇게 될 것 같은데? 정도를 가지고 풀 수 있는 문제가 아니다. 반대로 우리가 인과관계에 대해 이런 수준의 엄밀한 그림을 갖고 있지 않다면, 그리고 그것을 데이터를 통해 적절하게 검증하지 않았다면 인과관계에 대해 말하는 것은 마땅히 조심스러워야 한다. 복잡한 인과적 구조에 대한 지식도 검증도 부족하고 엄밀하지 않지만 편견과 짐작으로 그걸 메꿔 세상의 중요한 문제들에 대해 확신을 갖고 논하는 경우가 너무 많다.
